Как объяснить ребенку деление?

Проблемы с математикой в начальной школе возникают исключительно из-за пробелов в знаниях.

Простые арифметические действия, такие как сложение и вычитание, должны выполняться автоматически — если ученик испытывает определенные трудности, то нужно сначала проработать эту тему, прежде чем приступать к более сложным операциям.

Как объяснить ребенку деление? Начать с азов, использовать игры и нестандартный подход.

Подготовка к обучению

Для начала стоит убедиться в том, что школьник усвоил предыдущую программу и ничто не помешает ему освоить текущую. Стоит проверить следующие знания:

• числовые разряды (класс единиц и тысяч);

• состав числа;

• арифметические действия (сложение, вычитание);

• таблица умножения.

Именно последний пункт является ключевым. Если в этом вопросе не возникает сложностей, то достаточно объяснить ребенку, что деление является противоположной умножению операцией. Соответственно, нужно провести аналогичные действия, но в обратном порядке.

Операция деления: основные обозначения

Очень часто в задачах вопрос сформулирован следующим образом: «Найти частное чисел 30 и 5» или «Определить делитель, если частное 42, а делимое — 7». Если ребенок не знает обозначений, то он не сможет приступить к решению такого примера. Поэтому начинать нужно с основ:

• делимое — то число, которое и будет разделено;

• делитель — число, на которое будет разделено делимое;

• частное — результат.

Понять роль каждого показателя поможет простая игра. Есть 12 вкусных конфет, а в семье 4 человека. Как разделить сладости поровну? Всего 12 — это делимое. Количество человек — делитель. Ученику начальной школы будет легче понять задачу, если объяснить ему, что делимое всегда самое большое число. Невозможно разделить 4 на 12, а значит, пример будет выглядеть следующим образом: 12:4 = 3.

Как понять суть деления?

На начальном этапе проще всего объяснить деление как операцию, противоположную умножению. Если ребенок безупречно знает таблицу, то он будет совершать действия на автомате:

5*6 = 30, значит, если в задаче «делитель» — 30, а «делимое» — 6, то частное составит 5.

Стоит «поиграть» с ассоциациями: разделить фрукты, шоколадки, конфеты между всеми членами семьи. Часто детям нравятся примеры с деньгами, построенные по принципу: 

Было 28 гривен, купили 7 ручек, сколько стоит 1 ручка?

Такой подход позволит перейти от примеров на яблоках к работе непосредственно с числами.

Раскладываем число на компоненты

Работа с однозначными числами достаточно проста. Нужно выучить таблицу умножения и просто совершать действия в обратном порядке. Потребуется немного практики, чтобы научиться решать подробные примеры на скорость и в уме. Это будет полезно особенно при написании математических диктантов, когда учитель диктует задание, а детям нужно только записать правильный ответ.

Сложности наступают в тот момент, когда приходится решать примеры с теми числами, которые за пределами таблицы. Например:

Делимое — 90, делитель — 5. Нужно найти частное.

Ребенку сложно в уме выполнить требующиеся операции, поэтому нужно предложить ему разделить большое число на составляющие:

90 = 40+50;

40:5 + 50:5 = 8+10=18; значит 90:5=18.

Если ученик в первом классе хорошо усвоил состав числа, то у него не возникнет сложностей и с похожими операциями: 72 — это 60+12, 84 — это 60+24, 93 — это 30+30+30+3.

Деление в столбик

Такой тип примеров — один из любимых у детей. Он используется при работе с трех- и двузначными числами, которые сложно разделить в уме. Последовательность действий следующая:

Определить делимое и делитель: 648 — делимое, 36 — делитель. Записываем пример с помощью «уголка»: 

648|36; и начинаем подбирать значения, 36*2=72. 72 больше, чем 64, значит, этот вариант не подходит. 36*1=36, 36 меньше, чем 64 — это нужное нам число. Под 36 записываем 1. Продолжаем вести расчеты: 64-36=28, дописываем оставшееся число (648 — 64 мы уже использовали, осталось 8, которое мы и «сносим» к 28). Получается 288:36. Методом подбора определяем, что 36*10=360, 36*9=324, 36*8=288. Нужный результат получен, 288-288=0. Ответ:18. 

Перепроверяем себя, выполнив умножение в столбик или используя устный счет: 36*18, действительно получается 648 — ответ верный, все действия были выполнены правильно.

Деление с остатком

К этим вычислениям нужно приступать только тогда, когда предыдущий материал выучен безупречно, алгоритм решения детально разобран и действия выполняются за считанные минуты. Как только ребенок детально разобрался в вопросе, можно двигаться дальше.

Особенность деления с остатком в том, что нужно выделить основную часть и понять, какое же число останется в итоге. На начальных порах у школьника может возникнуть барьер, ведь до этого все примеры решались легко, а теперь нужен иной подход к вычислениям.

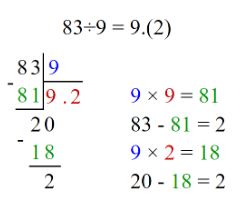Но опять-таки решение основывается на знании таблицы умножения и умении разделить большое число на несколько составляющих.

Пример: 

83:9, ребенок знает, что 81:9=9. 83-81=2. Значит, ответ: 9 и 2 в остатке.

114:5, 100:5=20, 10:5=2, 4 на 5 разделить невозможно. Соответственно, 114:5=100:5+20:5 и 4 = 22 и 4 в остатке.

Можно изучать этот тип примеров с помощью денежных операций, ведь сдача, полученная после оплаты покупок, — это как раз и есть остаток. Или же использовать для этой цели еду либо игрушки: куски торта, куклы можно делить на всех участников игрового процесса, подобрав такое количество, чтобы обязательно оставался «лишний» кусочек.

Дроби

Эта тема обычно является одной из самых сложных. А все потому, что школьникам сложно понять, почему 1 можно представить как 33 или 55. И хоть в школьной программе этому уделяется немало часов, многие ученики все-таки испытывают трудности. Деление простых чисел, операции в столбик, определение остатка — с этой задачей можно справиться и самостоятельно. Если же ученик «проседает» в дробях, то имеет смысл вернуться к истокам и повторно проработать простые арифметические действия.

Оптимальным решением станет обращение за помощью к квалифицированному педагогу, который поможет выявить причину сложностей и помочь с вычислениями. Например, найти в Запорожье курсы ментальной арифметики, благодаря которым цифры перестанут быть для детей чем-то пугающим, а большинство операций будут проводиться в уме. Такая подготовка позволит легко работать с дробями, выполняя сложение/вычитание, умножение/деление.

Деление дробей

Дробь — это число, которое состоит из нескольких частей. Например, всего 6 кусков торта: 66 , всего 6 и берем все эти 6 кусков. Если же всего 6, но взяли мы только 3, то дробь будет выглядеть: 36.

Для деления обыкновенных дробей используется метод перекрестных действий:

• числитель первого числа умножаем на знаменатель другого — результат станет числителем частного;

• знаменатель второго числа умножаем на числитель первого — результат становится знаменателем частного.

Сложность в том, что для деления используется умножение — это как раз обычно и смущает школьников. Поэтому правило нужно просто заучить, повторив его многократно и отработав на многочисленных примерах. Только в этом случае дети запоминают, что когда речь идет о дробях, для деления используется умножение (перемножаем расположенные по диагонали числа, а результат записываем в числитель/знаменатель частного).

Важные нюансы

В изучении арифметических действий очень важна последовательность. Нельзя учить малыша читать, пока он не выучил все буквы алфавита — путаница и постоянные ошибки не только будут мешать, но и могут раз и навсегда отбить охоту к чтению. С математикой аналогичная ситуация:

• нужно уметь правильно разделять большое число на несколько отдельных составляющих, с которыми проще провести требуемые операции;

• сложение и вычитание должны быть отработаны до автоматизма;

• к делению приступают только после тщательного изучения таблицы умножения.

Важно обратить внимание, что в качестве делимого выступает самое большое число — это поможет не запутаться при решении задач. А на ноль делить нельзя — подобный вопрос с подвохом часто встречается в заданиях, поэтому нужно не упустить этот момент.

Вывод

К каждому ребенку нужен свой подход — не существует единой методики, которая подойдет любому ученику. Кому-то проще оперировать цифрами, а примеры с яблоками или конфетами вызывают недоумение. Другие школьники по привычке считают на пальцах или на линейке — для них в качестве примера отлично подойдут задачи с покупками. Как объяснить ребенку деление? Начать с азов, пробовать разные методики, а если не удается достичь желаемого результата, довериться специалистам, обратиться к учителю или записаться на специализированные курсы, которые будут актуальны для детей в возрасте от 5 до 12 лет (подготовку к школе стоит начинать заблаговременно).